|
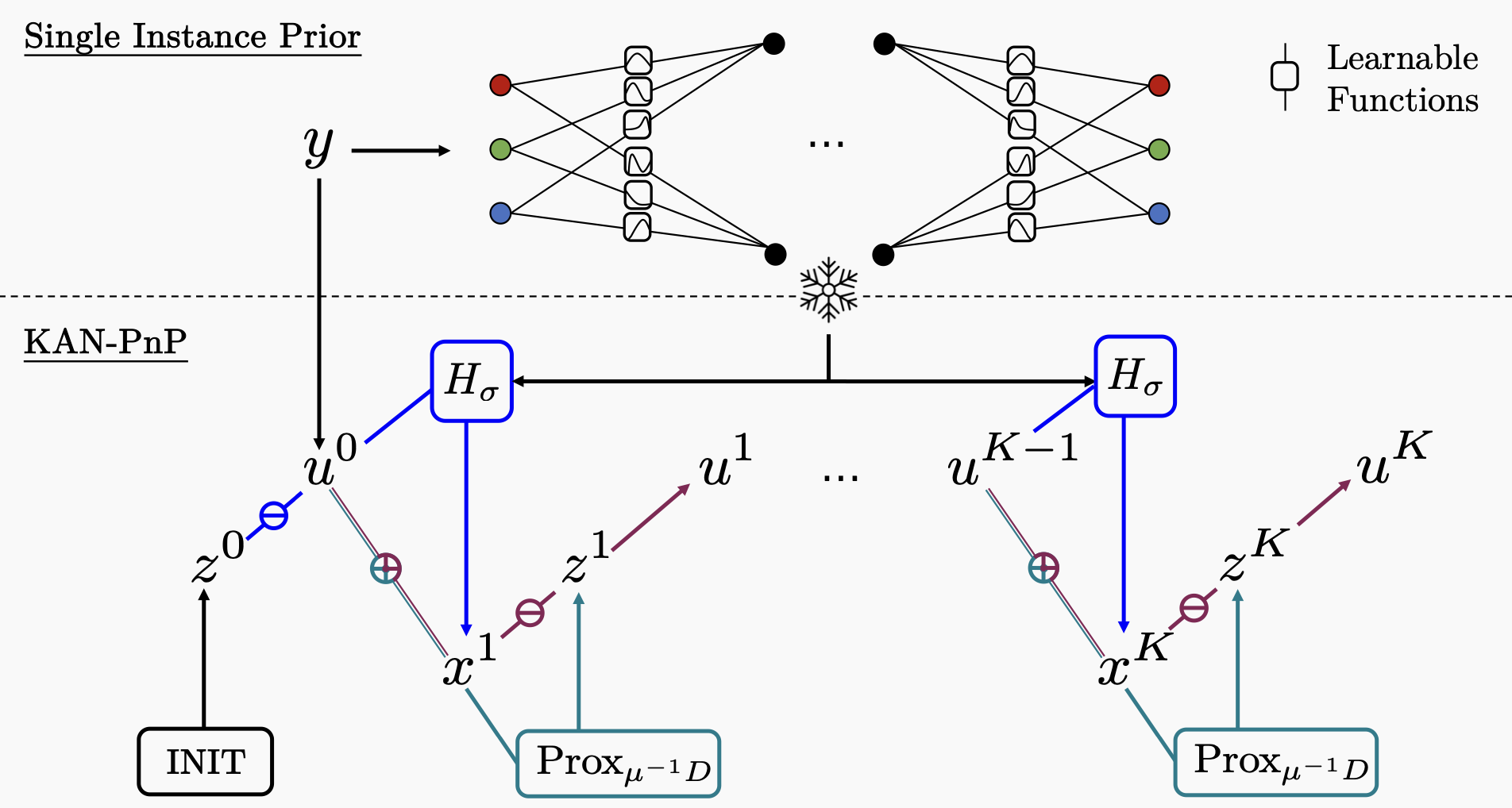
The use of Plug-and-Play (PnP) methods has become a central approach for solving inverse problems, with denoisers serving as regularising priors that guide optimisation towards a clean solution. In this work, we introduce KAN-PnP, an optimisation framework that incorporates Kolmogorov-Arnold Networks (KANs) as denoisers within the Plug-and-Play (PnP) paradigm. KAN-PnP is specifically designed to solve inverse problems with single-instance priors, where only a sin- gle noisy observation is available, eliminating the need for large datasets typically required by traditional denoising methods. We show that KANs, based on the Kolmogorov-Arnold representation theorem, serve effectively as priors in such set- tings, providing a robust approach to denoising. We prove that the KAN denoiser is Lipschitz continuous, ensuring stability and convergence in optimisation algo- rithms like PnP-ADMM, even in the context of single-shot learning. Additionally, we provide theoretical guarantees for KAN-PnP, demonstrating its convergence under key conditions: the convexity of the data fidelity term, Lipschitz continuity of the denoiser, and boundedness of the regularisation functional. These condi- tions are crucial for stable and reliable optimisation. Our experimental results show, on super-resolution and joint optimisation, that KAN-PnP outperforms exiting methods, delivering superior performance in single-shot learning with min- imal data. The method exhibits strong convergence properties, achieving high accuracy with fewer iterations. |